All you need to know about Carpenter's Square - 16
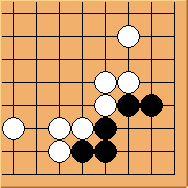
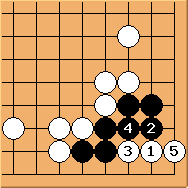
Black is blocked from the bottom side instead. This shape is commonly seen in real games. What can white do?
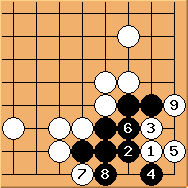
 is absolutely the key point. If black plays
is absolutely the key point. If black plays  ,
,  is good - it forces black to connect at
is good - it forces black to connect at  and at the same time creates a ko shape.
and at the same time creates a ko shape.
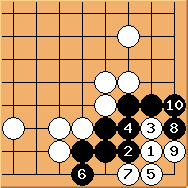
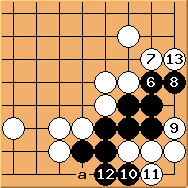
To continue,  is the correct answer.
is the correct answer.  is important to avoid a double-ko. The final result is an approach ko. White has to play 'a' first to make it a direct ko.
is important to avoid a double-ko. The final result is an approach ko. White has to play 'a' first to make it a direct ko.  cannot play
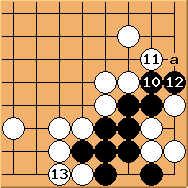
cannot play  - that would be a direct ko immediately.
- that would be a direct ko immediately.
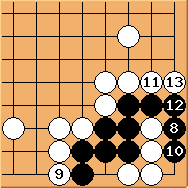
 may connect first.
may connect first.  is correct, recovering to the shape in Diagram 16.2.
is correct, recovering to the shape in Diagram 16.2.
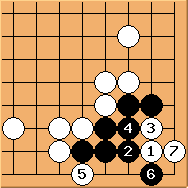
 here would be an overplay. Black would win the capturing race. Or ......
here would be an overplay. Black would win the capturing race. Or ......
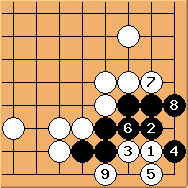
If white plays  here, the result is a seki.
here, the result is a seki.
 can also play the other side. Interestingly white can form a ko fight in a fashion similar to Diagram 16.2.
can also play the other side. Interestingly white can form a ko fight in a fashion similar to Diagram 16.2.
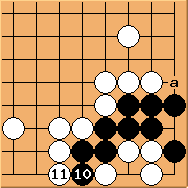
To continue, this results in a different approach ko (white needs to play 'a' first to make it a direct ko). So which one should black choose? Solution 1 or 2? The difference is very small. However, assume white manages to reach the direct ko stage (getting 'a' in Diagram 16.3 or 16.8), and black eventually wins the ko fight to live in the corner, black would be better off by 2 points if choosing Solution 1 (an easy way to validate this argument is to count the number of cross-sections black would occupy - 18 in Solution 1 and 17 in Solution 2).
Finally, it is important to remember  here won't work.
here won't work.  is good.
is good.
Unlike in Diagram 16.5, black is mysteriously short of liberty here.  has to play 'a' to form a ko. But that would be a failure because the ko is a direct ko.
has to play 'a' to form a ko. But that would be a failure because the ko is a direct ko.
Conclusion: black corner is not in immediately danger. There are two different ways to form approach ko. I recommend readers to remember the sequence in Diagram 16.2 and 16.3.